








2009-present. Professor, IRBI, (France)
1997-2009 : Assistant Professor, IRBI, (France)
2006. HDR (Ability to Lead Research), University Tours (France).
1996. PhD, University Bordeaux 1 (France).
1997-
2006. HDR (Ability to Lead Research), University Tours (France).
1996. PhD, University Bordeaux 1 (France).
Keywords:
Modelling; Population dynamics; EDP-EDO; Biological invasions; Physical ecology.
Modelling propagation in biological systems

My scientific activity is composed of different themes but they can be enclosed in a single title: " Propagation problems in biological systems ".
My current subject of research is biological invasions. The leafminer of the horse chestnut tree, Cameraria ohridella attacks trees by mining their leaves and is invading Europe. The leafminer is attacked by several parasitoids, but none of them is able to control its propagation. Infested chestnut trees turn completely yellow early summer, and lose almost all leaves.
The first approach I used was a discrete model showing the spatial propagation of leafminers and parasitoids in France. This model allowed us to predict the complete invasion of France in 2008. We have also studied the impact of the parasitoids on the dynamic of leafminers. Parasitoids are inefficient and the minimum parasitism rate should be at least equal to 25% to eradicate leafminers.
The second approach is a continuous model of reaction-diffusion (Magal et al. 2008). Let u(x,t) and v(x,t) denote the densities of leafminers (hosts) and parasitoids, and :
with f(u) = 1-(u/K 1), p(u) = Eu/(1+Ehu), g(v)=1-v/K 2, and where D = diffusion rate, r1 = growth rate of leafminers, r2 = growth rate of parasitoids, K1 = carrying capacity of leafminers, K2 = carrying capacity of parasitoids in absence of focal hosts, E = encounter rate, h = harvesting time, gamma = conversion efficiency.
I have studied the associated ordinary differential equations. This system leads to 3 possible issues: 1) persistence of leafminers, 2) control of leafminers by parasitoids, 3) possible control of leafminers depending on initial conditions. In general manner, the success of leafminers’ control increases with reservoir’s size of parasitoids. I also have made some numerical simulations of the partial differential equations system (Figure 1).
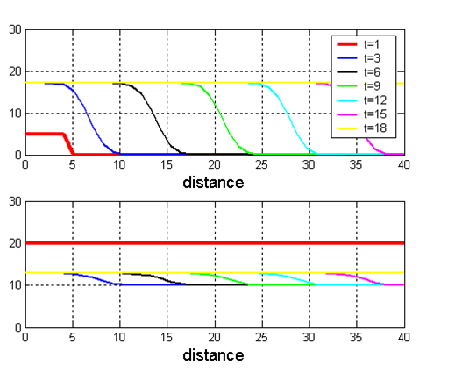
Figure 1. Spatial propagation of leafminers (above) and parasitoids (below). Parameters of the simulations are: D=1, r1=6, r2=3, K1=20, K2=10, E=0.5, h=0.8, gamma =0.8.
We have studied the effect of the diffusion rate on the propagation speed of leafminers. We have showed that the propagation speed of leafminers increases with the dispersion rate. But when the dispersion rate is too high, leafminers are eradicated by parasitoids. This is because diffusion dilutes leafminers. The parasitoids, which are generalist and present all over the domain, take them over in a second phase. The next step I am currently working on is to include alternative preys in the model. Indeed, parasitoids are generalists so they concentrate their attacks on several types of prey. So leafminers of horse chestnut tree may have an indirect impact on the density of alternative preys.
Before studying the leafminers of horse chestnut tree I have worked on an other lepidopteron, the leafminers of apple tree: Phyllonorycter ssp. (Lepidoptera : Gracillariidae). This leafminers is attacked by a parasitoid: Sympiesis sericeicornis (Hymenoptera : Eulophidae). Parasitoids and leafminers use vibration to locate each others (Djemaï et al. 2001, 2004). So I have studied the apple leaf as area of vibrations propagation.
In a first part, I have studied the propagation of vibrations using two lasers vibrometers. We have analysed signals generated by transients (impacts). Using wavelets, we have made a time-frequency analysis. We have showed that central nerve acts as a low-pass filter. Furthermore, energy lost through nerves with a diameter less than 0.4 mm was the same than energy lost through limb. This allowed us to construct a model of leaf taking into account only homogeneous regions and nerves with a diameter superior to 0.4mm (Magal et al. 2000).
In a second part we have studied the deformation of leaf submitted to an external force. This was done with a finite elements method (Figure 2).
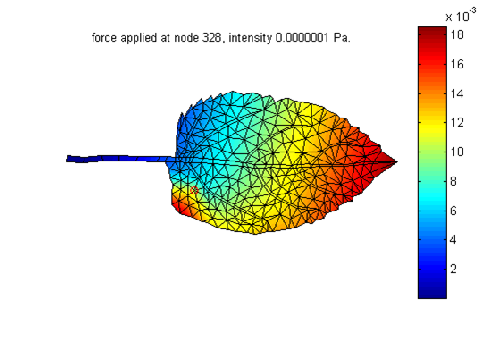
Figure 2. Amplitude deformation of a leaf submitted to an external punctual force.
I have also worked on a physical model simulating the movement of crickets' hairs (Magal et al. 2006). Indeed, crickets' hairs are used as mechanoreceptors to escape from predation. Hairs are deflected by the air flow caused by predators. This model is based on concepts of fluid and solid mechanics. Hair is considered as an inversed pendulum. We measure angle deflections quantifying hair's response. A real distribution of hairs allows us to calculate the response of the entire canopy of a cercus. This model is useful to understand mechanisms of vibratory signals reception, but also to compare the different instars of crickets.

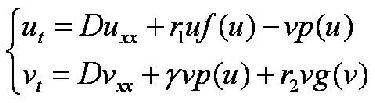



Publication List
L. Desutter-Grandcolas, E. Blanchet, T. Robillard, C. Magal, F. Vannier and O. Dangles ( 2010). Evolution of the cercal sensory system in a tropical cricket clade (Orthoptera: Grylloidea: Eneopterinae): a phylogenetic approach. Biological Journal of the Linnean Society, 99, 614-631.
1. Magal C., Cosner C., Ruan S. & Casas J. (2008). Control of invasive hosts by generalist parasitoids. Mathematical Medicine and Biology, 25: 1-20.
2. Casas J., Magal C. & Sueur J. (2007). Dispersive and non-dispersive waves through plants: implications for arthropod vibratory communication. Proceedings of the Royal Society of London B, 274: 1087-1092.
3. Dangles O., Pierre D., Magal C., Vannier F & Casas J. (2006). Ontogeny of air-motion sensing in cricket. Journal of Experimental Biology, 209: 4363-4370.
4. Magal C., Dangles O., Caparroy P. & Casas J. (2006). Hair canopy of cricket sensory system tuned to predator signal. Journal of Theoretical Biology, 241: 459-466.
5. Casas J. & Magal C. (2006). Vibratory communication in host-parasitoid systems: from plant biomechanics to behavioral in "Insect Sounds & Communication" (book chapter).
4. Magal C., Dangles O., Caparroy P. & Casas J. (2006). Hair canopy of cricket sensory system tuned to predator signal. Journal of Theoretical Biology, 241: 459-
5. Casas J. & Magal C. (2006). Vibratory communication in host-
6. Dangles O., Magal C., Pierre D., Olivier A. & Casas J. (2005). Variation in morphology and performance of predator-sensing system in wild cricket populations. Journal of Experimental Biology, 208: 461-468.
7. Djemai I., Casas J. & Magal C. (2004). Parasitoid foraging decisions mediated by artificial vibrations. Animal Behaviour, 67: 567-571.
8. Djemai I., Casas J. & Magal C. (2001). Matching host reactions to parasitoid wasp vibrations. Proceedings of the Royal Society of London B, 268: 2403-2408.
7. Djemai I., Casas J. & Magal C. (2004). Parasitoid foraging decisions mediated by artificial vibrations. Animal Behaviour, 67: 567-
8. Djemai I., Casas J. & Magal C. (2001). Matching host reactions to parasitoid wasp vibrations. Proceedings of the Royal Society of London B, 268: 2403-
9. Suppo C., Naulin J-M., Langlais M. & Artois M. ( 2000). A modelling approach of vaccination and contraception programs for rabies control in fox populations. Proceedings of the Royal Society of London B, 267: 1575-1582 .
10. Magal C., Casas J., Schöeller M. & Tautz J. (2000). The role of leaf structure in vibration propagation. J. Acoust. Soc. Am., 108(5): 2412-2418 .
11. Langlais M. & Suppo C. (2000). Remarks on a generic SEIRS model and application to two cat retroviruses and fox rabies. Mathematical and computer modelling, 31: 117-124 .
12. Courchamp F., Suppo C., Fromont E. & Bouloux C. (1997). Population Dynamics of two Feline Retroviruses (FIV and FeLV) within a Population of Cats. Proceedings of the Royal Society of London B, 264: 785-794.
13. Dordan O. & Suppo C. (1997). Qualitative analysis applied to population dynamics. Journal of Biological Systems, 5(1) and 5(2).
13. Dordan O. & Suppo C. (1997). Qualitative analysis applied to population dynamics. Journal of Biological Systems, 5(1) and 5(2).
14. Artois M., Langlais M. & Suppo C. (1997). Simulations of rabies control within an increasing fox population. Ecological Modelling, 97: 23-34.

Institut de Recherche sur la Biologie de l'Insecte
UMR 7261 Faculté des Sciences et Techniques
Avenue Monge, Parc Grandmont
37200 TOURS (France)

Keywords :
Modelling
Population dynamics
EDP-EDO
Biological invasions
Physical ecology
